Fractals Fractals

Fractals


The term 'fractal' was coined by mathematician Benoit Mandelbrot to denote a geometry which traces inherent order in chaotic shapes and processes. A fractal is a geometric object created from a specific type of mathematical formula. Fractals are characterized by repetition and self-similarity, at any level of magnification. They have strong distinguishing characteristics and visual motifs, often featuring loops, arcs, spirals, and other shapes and revealing increasing detail as you zoom into the fractal structure.

Koch Snowflake


One of the more intuitive sets of this form which shows self-similarity is the set whose graph is called a Koch snowflake.

This set is drawn using very simple geometric rules. We begin with a line in which the middle third is replaced by two line segments which form two sides of an equilateral triangle, as shown below. By pressing the "Add a Level " button you may continue the process by replacing the middle third of each line segment by two sides of an equilateral triangle. This can be continued many times in this program and the Koch curve itself is the result of continuing this an infinite number of steps. The fractal is self-similar, since if we enlarged any single line segment at any step it would have the same property as the larger part. You may also animate the procedure by pressing tne "Animate" button.


 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

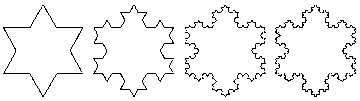
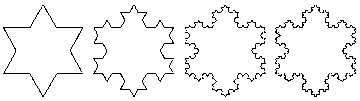
The Koch snowflake fractal has another interesting property common to fractals in that it has a 'fractal dimension'. Lines have dimension 1, squares have dimension 2, and cubes have dimension 3, but the limiting Koch function has dimension approximately 1.2618, a dimension higher than that of a line(1), but less than that of a square(2), since the figure does not fill the plane.

If a self-similar figure contains n copies of itself and each copy has length s, then the fractal dimension D is defined to be ln(n)/ln(1/s). In this case each segment contains 4 copies of itself and each copy is 1/3 as long as the previous length.

So D = ln(4)/ln(1(1/3)) = ln(4)/ln(3)= 1.2618595071429148


Mandelbrot Set


One of the more complex fractals is the Mandelbrot set which is shown below.

You can see an interactive version of the Mandelbrot set here.

In this interactive version you can see for yourself the self-similarity property by clicking on this graph with the left button of the mouse, then dragging the mouse a short distance away and releasing. You will then see the small section you have chosen enlarged to fill the graph.

You can also see the complexity in the following two YouTube videos which zoom into the Mandelbrot set to a great depth.

Note in this video the recurring Mandelbrot sets which appear as it zooms in further and further.


In this video the final area is covers a very small fraction of the area of the beginning area (about 1/10^72 = 0.000...0001 with 72 zeroes in that number.) Even deeper levels can be computed, but there are limitations with the size of the numbers the computer can manipulate.

These seemingly chaotic graphs are formed by a very simple mathematical process. Go to the mathematics link for a short description of the mathematics behind the Mandelbrot set.

Julia Set


A related set is the Julia set. Julia sets are different in that a particular constant used in the calculation yields a completely different graph. The mathematics in this case is very similar to that of the Mandelbrot set except that the same constant c is used for the entire computation.

You can see an interactive version of the Julia Set here. Again you can show the self-similarity by dragging a rectangle across any section of the graph you wish to enlarge.

Some examples are shown in the following video which demonstrates some of these Julia sets. The various constants used are points from the Mandelbrot set.

Newton's Method


Another interesting fractal is that formed by using Newton's method to find the cube roots of 1 in the complex plane. The equation f(z) = z^3 - 1 for complex z has three solutions, the three cube roots of 1. We will start with any point in the complex plane and then we will use the Newton-Raphson technique to determine which of the three cube roots this technique converges to. You can see an interactive version of Newton's method fractal here. Again you can show the self-similarity by dragging a rectangle across any section of the graph you wish to enlarge.

Every point which converges by this method to z=1 will be colored red. The points which converge to the other two complex sroots will be colored green and blue respectively. This will create three basins of attraction in the three colors. Again, you can see the self-similarity by dragging a rectangle and clicking the Redraw button.

Some of the mathematics of this technique may be further studied in Example 2 of the link to a website on chaos.

Iterated Function Systems

Iterated Function Systems are used to form some pictures like the Sierpinski triangle, which is created by applying a set of three functions, or transformations, to the points contained in a triangle.

The mathematics of the creation of a Sierpinski triangle by an Iterated Function System can be further examined at this link.

Another example is a set of four functions, which when iterated, yields the Barnsley fern.

See how it is implemented here

The following video zooms into the Barnsley fern to show the self-similarity-i.e.-each leaf is similar to the whole fern and each branch on each leaf is also similar to the whole fern.

Iterated Function Systems can be used to produce other fractals as well, such as the 3 dimensional Menger sponge.


L-Systems



L-Systems are used to generate tree-like shapes and other self-similar pictures. To see how this is formed, look at a bush formed recursively To study the method of forming this bush, see the L-System link.

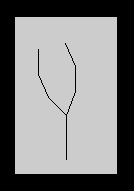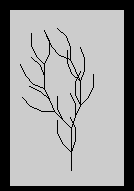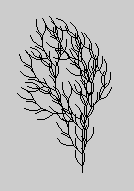
Some rather realistic plants can be drawn with L-Systems, such as the 'weeds' below:

A number of L-Systems fractals are available here with the formulas which generate them.

Bifurcation


Another fractal which shows self-similarity is the bifurcation shown in the logistic equation

xnew = xold*r*(1-r).

The mathematics of this technique may be further studied in Example 1 of the link to a website on chaos.