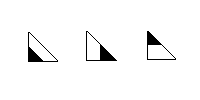
(1) x' = 0.5x and y' = 0.5yGeometrically, the effect of each of these transformations can be shown in the following graphs. Suppose we start with a triangle with vertices at (0,0), (1,0), and (0,1).
(2) x' = 0.5x + 0.5 and y' = 0.5y
(3) x' = 0.5x and y' = 0.5y + 0.5
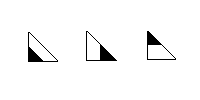
The first transformation takes any point (x,y) to (0.5x, 0.5y), so (0,0) remains (0,0), while (1,0) is transformed to (0.5, 0) and (0,1) to (0, 0.5), which are vertices of the shaded part of the first triangle. Check to see that the other two transformations take the whole triangle to one of the shaded triangles. Now, to draw the Siepinski triangle, we begin with a random point inside the triangle and randomly choose one of the transformations. Plot the transformed point and continue this process until 5000 points are drawn. Although the points are selected randomly, the drawing will be essentially the same each time. This is true since the first point will be transformed to a point in one of the three shaded areas defined by the three transformations above and never to the white area in the center of the original triangle.
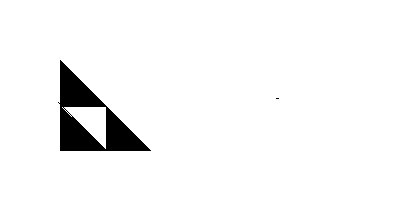
The same principle now applies to the second point. It will be transformed to one of the points shaded black in the following diagram and never to any of the white areas.
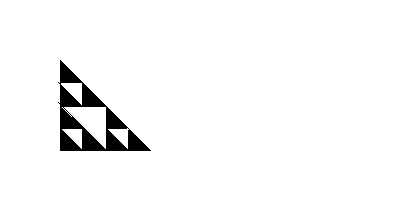
This process continues as the points are drawn to make the Sierpinski triangle we have seen earlier.