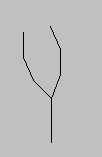
1) "sentence" = "subject" "verb" 2) "subject" = Dick | Jane | Tom 3) "verb" = runs | talks
The terms in quotes are called non-terminals and the others are called terminals. If "sentence" is the starting non-terminal, we replace it by the two non-terminals "subject" and "verb". Then we may replace "subject" by Dick or Jane or Tom and "verb" by either runs or talks to get "sentences" like 'Dick runs', or 'Jane talks' or any other combination.
For L-systems we start with the beginning rule
F
and the only other rule is
F = FF+[+F-F-F]-[-F+F+F]
As you can imagine, these strings quickly become very long since it is recursive because F is replaced by a string which also involves F. The first application replaces the one character by 20 characters. Since there are 8 F's in the string, a second application of the rule gives 8x20+12 or 172 characters. At the next stage, we would replace each of the 160 F's by the 20 character string, making it more that 3200 characters long.
How is this interpreted graphically to draw the bush we have seen? If we interpret the 'F' as a command to go forward a given distance and '+' a command to turn right 22.5 degrees and '-' to turn left the same. The brackets are used to mark places to return to and allow 'branches' to be drawn.
Thus the first FF draws the given length twice to form the trunk of the bush. We then turn right 22.5 degrees, save that location, and turn right, move forward, turn left, move forward, turn left, and move forward before returning to the spot we saved earlier. This has formed the right branch of the bush. Now we form the left branch by turning left, saving the location, turning left, moving forward, turning right, moving forward, turning right one more time and moving forward a final time.
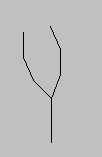
By decreasing the scale and replacing each of the F's by the same string, we increase the complexity of the drawing as shown here: