As defined by Chris Langton, one of its founders, artificial life is a field of study devoted to understanding life by attempting to abstract the fundamental dynamical principles underlying biological phenomena, and recreating these dynamics in other physical media, such as computers, making them accessible to new kinds of experimental manipulation and testing.
There are different forms of artificial life, most of which are described in the sections listed below.
The simplest cellular automaton is the one-dimensional form, which is merely a linear set of cells in one of two states. There is also a set of rules to show how the next generation of the automaton appears. We will indicate the states by drawing them as black or white. To show how they "grow" we will draw successive generations of the states of the automaton directly underneath one another. For example, if the rule is that a cell "dies" if both of its neighbors are dead or if both are alive. A cell will be alive in the next generation if one of its two neighbors is alive and one is dead. If we begin with one "live" cell and apply the rule suggested, we have the following 8 generations.
More generations of the same automaton on a different scale would yield
Slightly more complicated one-dimensional cellular automata which depend on the states of the two neighbors and the former state of the present cell may yield generations such as the following.
A working sample is found at the CA link which demonstrates the formation of generations of the cellular automaton. Read the first page and then go to the cellular atomataton generator on the next page. To get a form of the Sierpinski triangle from Rule 16 , click on the boxes representing 16 and 2 (18 base 10 = 00010010 base 2) and then generate the automaton. Check to see if Rule 90 also represents the Sierpinski traingle and matches the verbal form of the rule expressed above.
For more detailed information, check the articles by Stephen Wolfram, especially the 1983 paper on cellular automata.
The best known form of the two-dimensional cellular automaton is
that given by John Conway in his Game of Life. The cellular automaton
here is two dimensional and the rules are simple. Each cell
has eight neigbors and the life in that cell for the next
generation depends on the number of its neigboring cells which are alive.
A new cell is born when there are 3 live neighbors, a cell stays
alive when there are 2 or 3 live neighbors, and it dies of either solitude or
overpopulation in other cases. These simple rules
can give rise to many interesting patterns, some of which move and
grow and give rise to other patterns.
For a working version of the game of life see
this site.
Click on three of the cells to form this pattern: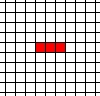 
and then click Start.
For a more interesting automaton, click Stop, Clear, and then form this pattern: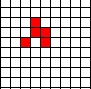 
. Click start again to see a "glider" move.
Check this link for much more detail and links to other pages.
There is a Java applet which shows boids in action.
Flocking is a particularly good example of a complex global behavior which can arise from the interaction of simple local rules. This behavior is typical of flocks of birds, schools of fish, and herds of animals. These rules were used to show the action of the herds of wildebeests in the Lion King movie.
Another example of a simulation of life's complex patterns with simple rules is a simulation of ants and food supply. Go to this site and click the mouse on the simulation in the upper right hand corner. This simulates dropping a breadcrumb, which a few ants will find in their random search.